p = [1 7 0 -5 9];
Evaluating Polynomials
The polyval function is used for evaluating a polynomial at a specified value. For example, to evaluate our previous polynomial p, at x = 4, type −p = [1 7 0 -5 9]; polyval(p,4)MATLAB executes the above statements and returns the following result −
ans = 693MATLAB also provides the polyvalm function for evaluating a matrix polynomial. A matrix polynomial is a polynomial with matrices as variables.
For example, let us create a square matrix X and evaluate the polynomial p, at X −
p = [1 7 0 -5 9]; X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8]; polyvalm(p, X)MATLAB executes the above statements and returns the following result −
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269
Finding the Roots of Polynomials
The roots function calculates the roots of a polynomial. For example, to calculate the roots of our polynomial p, type −p = [1 7 0 -5 9]; r = roots(p)MATLAB executes the above statements and returns the following result −
r = -6.8661 + 0.0000i -1.4247 + 0.0000i 0.6454 + 0.7095i 0.6454 - 0.7095iThe function poly is an inverse of the roots function and returns to the polynomial coefficients. For example −
p2 = poly(r)MATLAB executes the above statements and returns the following result −
p2 = Columns 1 through 3: 1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i Columns 4 and 5: -5.00000 - 0.00000i 9.00000 + 0.00000i
Polynomial Curve Fitting
The polyfit function finds the coefficients of a polynomial that fits a set of data in a least-squares sense. If x and y are two vectors containing the x and y data to be fitted to a n-degree polynomial, then we get the polynomial fitting the data by writing −p = polyfit(x,y,n)
Example
Create a script file and type the following code −x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data p = polyfit(x,y,4) %get the polynomial % Compute the values of the polyfit estimate over a finer range, % and plot the estimate over the real data values for comparison: x2 = 1:.1:6; y2 = polyval(p,x2); plot(x,y,'o',x2,y2) grid onWhen you run the file, MATLAB displays the following result −
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250
And plots the following graph −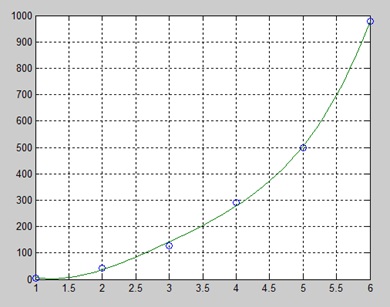

No comments:
Post a Comment