LISP - Tree

You can build tree data structures from cons cells, as lists of lists.
To implement tree structures, you will have to design functionalities that would traverse through the cons cells, in specific order, for example, pre-order, in-order, and post-order for binary trees.

Tree as List of Lists

Let us consider a tree structure made up of cons cell that form the following list of lists:
((1 2) (3 4) (5 6)).
Diagrammatically, it could be expressed as:

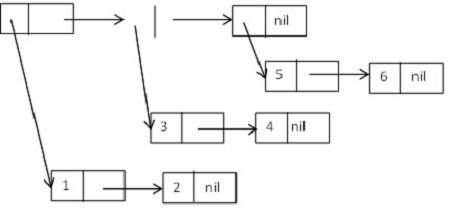
Tree Functions in LISP

Although mostly you will need to write your own tree-functionalities according to your specific need, LISP provides some tree functions that you can use.
Apart from all the list functions, the following functions work especially on tree structures:

Function	Description
copy-tree x & optional vecp	It returns a copy of the tree of cons cells x. It recursively copies both the car and the cdr directions. If x is not a cons cell, the function simply returns x unchanged. If the optional vecp argument is true, this function copies vectors (recursively) as well as cons cells.
tree-equal x y & key :test :test-not :key	It compares two trees of cons cells. If x and y are both cons cells, their cars and cdrs are compared recursively. If neither x nor y is a cons cell, they are compared by eql, or according to the specified test. The :key function, if specified, is applied to the elements of both trees.
subst new old tree & key :test :test-not :key	It substitutes occurrences of given old item with new item, in tree, which is a tree of cons cells.
nsubst new old tree & key :test :test-not :key	It works same as subst, but it destroys the original tree.
sublis alist tree & key :test :test-not :key	It works like subst, except that it takes an association list alist of old-new pairs. Each element of the tree (after applying the :key function, if any), is compared with the cars of alist; if it matches, it is replaced by the corresponding cdr.
nsublis alist tree & key :test :test-not :key	It works same as sublis, but a destructive version.

Example 1

Create a new source code file named main.lisp and type the following code in it.

(setq lst (list '(1 2) '(3 4) '(5 6)))
(setq mylst (copy-list lst))
(setq tr (copy-tree lst))

(write lst)
(terpri)
(write mylst)
(terpri)
(write tr)

When you execute the code, it returns the following result:

((1 2) (3 4) (5 6))
((1 2) (3 4) (5 6))
((1 2) (3 4) (5 6))

Example 2

Create a new source code file named main.lisp and type the following code in it.

(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9)))))
(write tr)
(setq trs (subst 7 1 tr))
(terpri)
(write trs)

When you execute the code, it returns the following result:

((1 2 (3 4 5) ((7 8) (7 8 9))))
((7 2 (3 4 5) ((7 8) (7 8 9))))

Building Your Own Tree

Let us try to build our own tree, using the list functions available in LISP.

First let us create a new node that contains some data

(defun make-tree (item)
   "it creates a new node with item."
   (cons (cons item nil) nil)
)

Next let us add a child node into the tree - it will take two tree nodes and add the second tree as the child of the first.

(defun add-child (tree child)
   (setf (car tree) (append (car tree) child))
   tree)

This function will return the first child a given tree - it will take a tree node and return the first child of that node, or nil, if this node does not have any child node.

(defun first-child (tree)
   (if (null tree)
      nil
      (cdr (car tree))
   )
)

This function will return the next sibling of a given node - it takes a tree node as argument, and returns a reference to the next sibling node, or nil, if the node does not have any.

(defun next-sibling (tree)
   (cdr tree)
)

Lastly we need a function to return the information in a node:

(defun data (tree)
   (car (car tree))
)

Example

This example uses the above functionalities:
Create a new source code file named main.lisp and type the following code in it.

(defun make-tree (item)
   "it creates a new node with item."
   (cons (cons item nil) nil)
)
   (defun first-child (tree)
      (if (null tree)
         nil
         (cdr (car tree))
      )
   )

(defun next-sibling (tree)
   (cdr tree)
)
(defun data (tree)
   (car (car tree))
)
(defun add-child (tree child)
   (setf (car tree) (append (car tree) child))
   tree
)

(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9)))))
(setq mytree (make-tree 10))

(write (data mytree))
(terpri)
(write (first-child tr))
(terpri)
(setq newtree (add-child tr mytree))
(terpri)
(write newtree)

When you execute the code, it returns the following result:

10
(2 (3 4 5) ((7 8) (7 8 9)))

((1 2 (3 4 5) ((7 8) (7 8 9)) (10)))