Data Structure & Algorithms - Spanning Tree

A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected..

By this definition, we can draw a conclusion that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices.
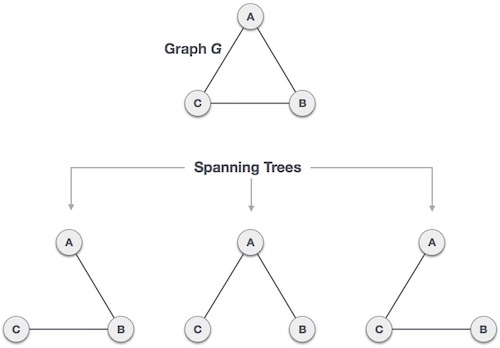We found three spanning trees off one complete graph. A complete undirected graph can have maximum n^n-2 number of spanning trees, where n is the number of nodes. In the above addressed example, 3³⁻² = 3 spanning trees are possible.

General Properties of Spanning Tree

We now understand that one graph can have more than one spanning tree. Following are a few properties of the spanning tree connected to graph G −

• A connected graph G can have more than one spanning tree.
• All possible spanning trees of graph G, have the same number of edges and vertices.
• The spanning tree does not have any cycle (loops).
• Removing one edge from the spanning tree will make the graph disconnected, i.e. the spanning tree is minimally connected.
• Adding one edge to the spanning tree will create a circuit or loop, i.e. the spanning tree is maximally acyclic.

Mathematical Properties of Spanning Tree

• Spanning tree has n-1 edges, where n is the number of nodes (vertices).
• From a complete graph, by removing maximum e - n + 1 edges, we can construct a spanning tree.
• A complete graph can have maximum n^n-2 number of spanning trees.

Thus, we can conclude that spanning trees are a subset of connected Graph G and disconnected graphs do not have spanning tree.

Application of Spanning Tree

Spanning tree is basically used to find a minimum path to connect all nodes in a graph. Common application of spanning trees are −

• Civil Network Planning
• Computer Network Routing Protocol
• Cluster Analysis

Let us understand this through a small example. Consider, city network as a huge graph and now plans to deploy telephone lines in such a way that in minimum lines we can connect to all city nodes. This is where the spanning tree comes into picture.

Minimum Spanning Tree (MST)

In a weighted graph, a minimum spanning tree is a spanning tree that has minimum weight than all other spanning trees of the same graph. In real-world situations, this weight can be measured as distance, congestion, traffic load or any arbitrary value denoted to the edges.

Minimum Spanning-Tree Algorithm

We shall learn about two most important spanning tree algorithms here −

• Kruskal's Algorithm
• Prim's Algorithm

Both are greedy algorithms.