Profit Margin Formula in Excel

 Calculating gross profit margin, operating profit margin and net profit margin in Excel is easy. Simply use the formulas explained on this page.

Gross Profit Margin

Assume your business had a total revenue of $10,000 in July and the cost of goods sold (COGS) equaled $4,000.

To calculate the gross profit margin, use the following formula:

Gross Profit Margin	=	Total Revenue - COGS
		Total Revenue

1. The formula below calculates the number above the fraction line. This is called the gross profit.

2. Divide this result by the total revenue to calculate the gross profit margin in Excel.

3. On the Home tab, click the percentage symbol to apply a Percentage format.

Result:

Operating Profit Margin

The operating profit margin also includes operating expenses (OPEX) such as rent, equipment, inventory costs, marketing, etc.

To calculate the operating profit margin, use the following formula:

Operating Profit Margin	=	Total Revenue - COGS - OPEX
		Total Revenue

1. The formula below calculates the number above the fraction line. This is called the operating profit.

2. Divide this result by the total revenue to calculate the operating profit margin in Excel.

3. On the Home tab, click the percentage symbol to apply a Percentage format.

Result:

Net Profit Margin

The net profit margin also includes non-operating expenses such as interest (on debt) and taxes.

To calculate the net profit margin, use the following formula:

Net Profit Margin	=	Total Revenue - COGS - OPEX - I - T
		Total Revenue

where:

COGS = Cost of Goods Sold

OPEX = Operating expenses

I = Interest

T = Taxes

1. The formula below calculates the number above the fraction line. This is called the net income.

2. Divide this result by the total revenue to calculate the net profit margin in Excel.

3. On the Home tab, click the percentage symbol to apply a Percentage format.

Result:

Conclusion: a 35% net profit margin means your business has a net income of $0.35 for each dollar of sales.

 

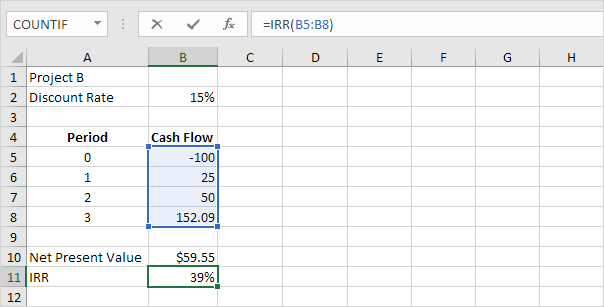
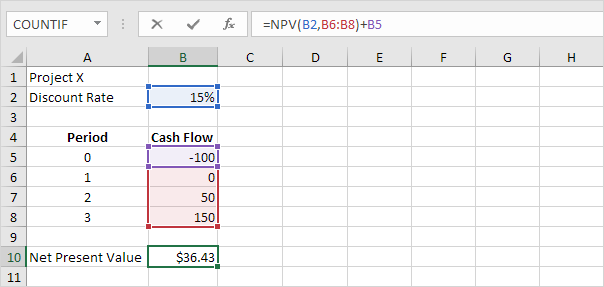
Depreciation Formulas in Excel

 

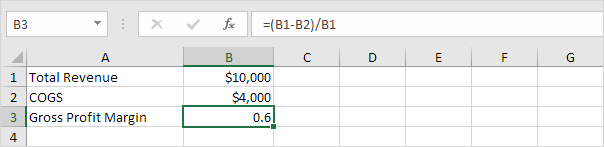
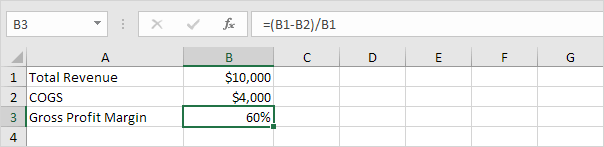
Excel offers five different depreciation functions. We consider an asset with an initial cost of $10,000, a salvage value (residual value) of $1000 and a useful life of 10 periods (years). Below you can find the results of all five functions. Each function will be explained separately in the next 5 paragraphs.

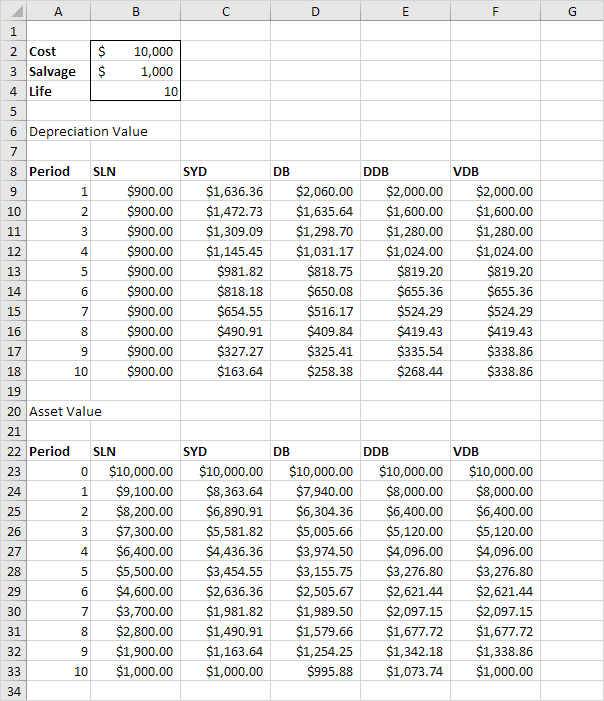
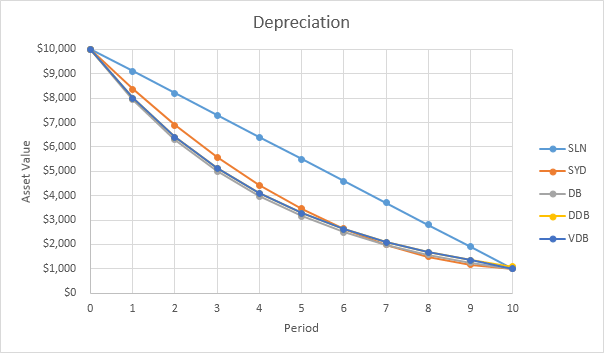
Most assets lose more value in the beginning of their useful life. The SYD, DB, DDB and VDB functions have this property.

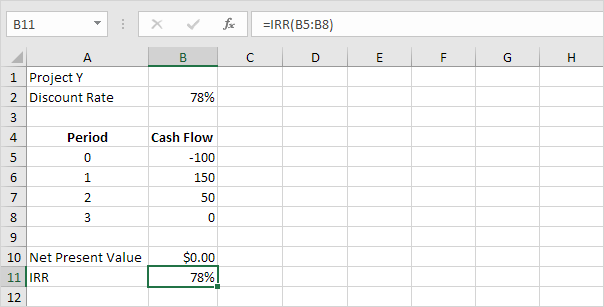
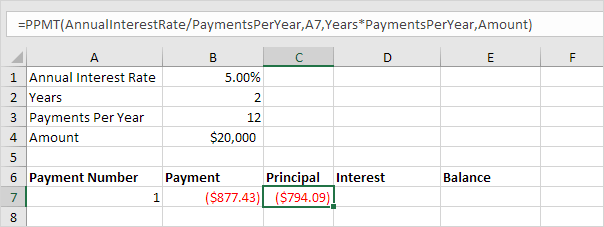
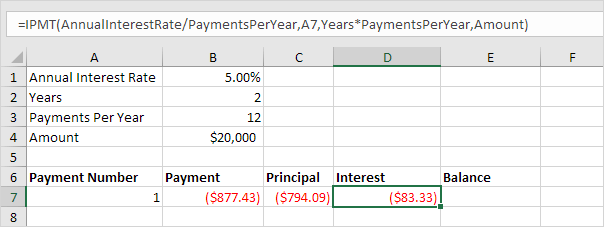
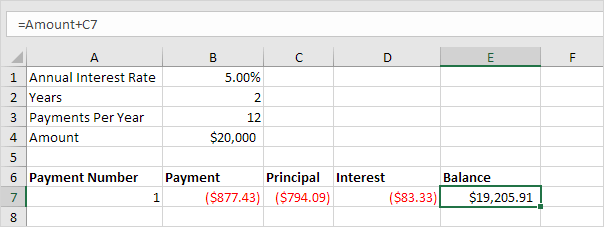
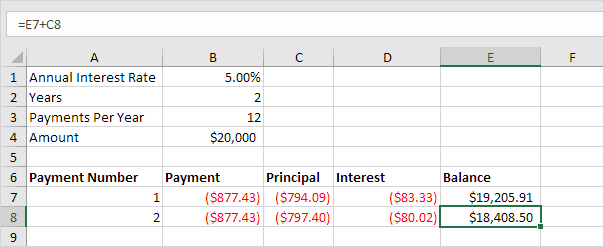
SLN

The SLN (Straight Line) function is easy. Each year the depreciation value is the same.

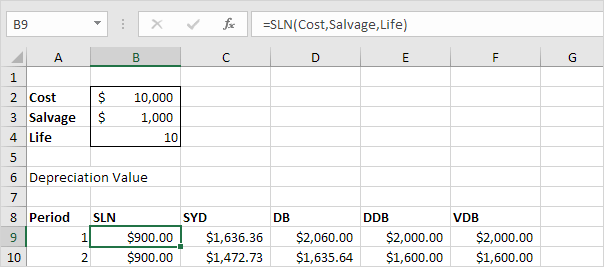
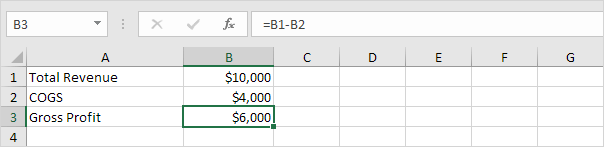
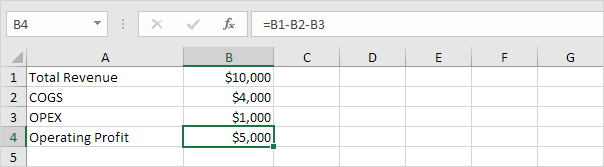
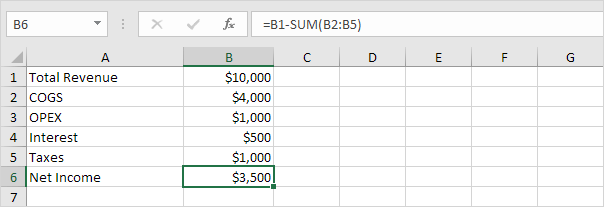
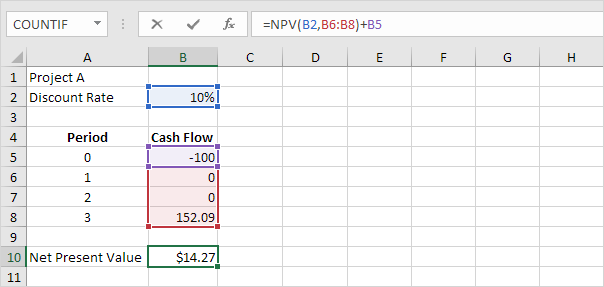
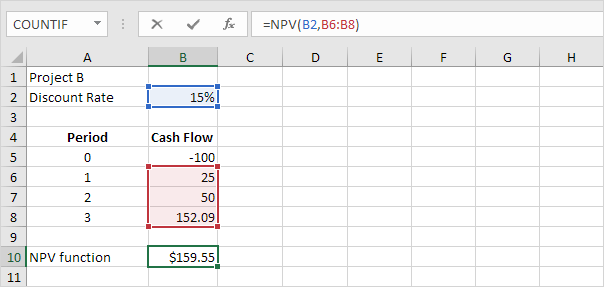
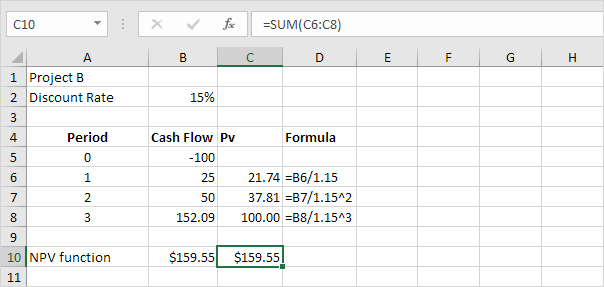
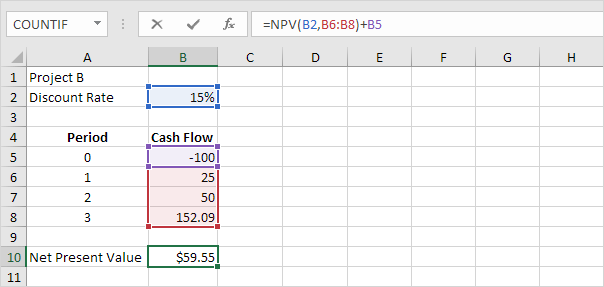
The SLN function performs the following calculation. Depreciation Value = (10,000 - 1,000) / 10 = 900.00. If we subtract this value 10 times, the asset depreciates from 10,000 to 1000 in 10 years (see first picture, bottom half).

SYD

The SYD (Sum of Years' Digits) function is also easy. As you can see below, this function also requires the period number.

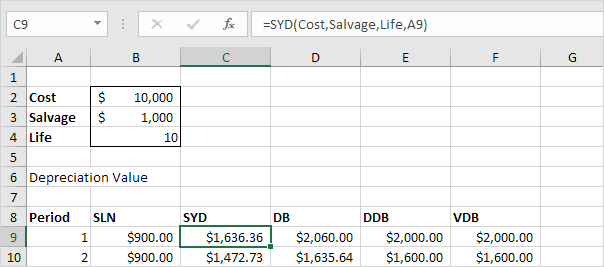
The SYD function performs the following calculations. A useful life of 10 years results in a sum of years of 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 55. The asset loses 9000 in value. Depreciation value period 1 = 10/55 * 9000 = 1,636.36. Depreciation value period 2 = 9/55 * 9000 = 1,472.73, etc. If we subtract these values, the asset depreciates from 10,000 to 1000 in 10 years (see first picture, bottom half).

DB

The DB (Declining Balance) function is a bit more complicated. It uses a fixed rate to calculate the depreciation values.

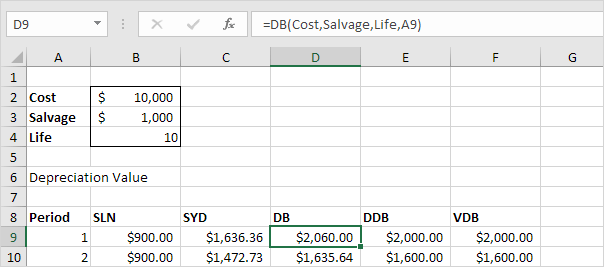
The DB function performs the following calculations. Fixed rate = 1 - ((salvage / cost) ^ (1 / life)) = 1 - (1000/10,000)^(1/10) = 1 - 0.7943282347 = 0.206 (rounded to 3 decimal places). Depreciation value period 1 = 10,000 * 0.206 = 2,060.00. Depreciation value period 2 = (10,000 - 2,060.00) * 0.206 = 1635.64, etc. If we subtract these values, the asset depreciates from 10,000 to 995.88 in 10 years (see first picture, bottom half).

Note: the DB function has a fifth optional argument. You can use this argument to indicate the number of months to go in the first year (If omitted, it is assumed to be 12). For example, set this argument to 9 if you purchase your asset at the beginning of the second quarter in year 1 (9 months to go in the first year). Excel uses a slightly different formula to calculate the depreciation value for the first and last period (the last period represents an 11th year with only 3 months).

DDB

The DDB (Double Declining Balance) function is easy again. However, sometimes you don't reach the salvage value when you use this function.

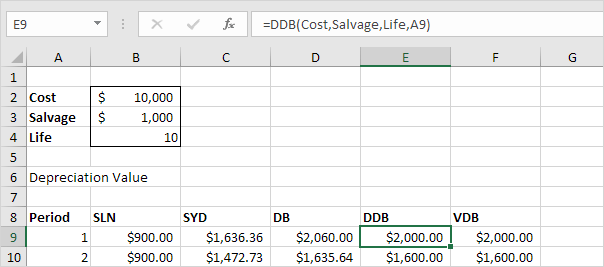
The DDB function performs the following calculations. A useful life of 10 years results in a rate of 1/10 = 0.1. Because this function is called Double Declining Balance we double this rate (factor = 2). Depreciation value period 1 = 10,000 * 0.2 = 2,000.00. Depreciation value period 2 = (10,000 - 2,000.00) * 0.2 = 1600.00, etc. As said earlier, sometimes you don't reach the salvage value when you use this function. In this example, if we subtract the depreciation values, the asset depreciates from 10,000 to 1073.74 in 10 years (see first picture, bottom half). However, read on to fix this.

Note: the DDB function has a fifth optional argument. You can use this argument to use a different factor.

VDB

The VDB (Variable Declining Balance) function uses the DDB (Double Declining Balance) method by default. The 4th argument indicates the starting period, the 5th argument indicates the ending period.

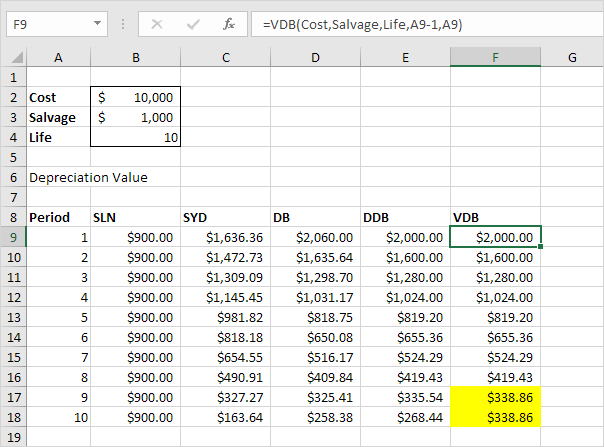
The VDB function performs the same calculations as the DDB function. However, it switches to Straight Line calculation (yellow values) to make sure you reach the salvage value (see first picture, bottom half). It only switches to Straight Line calculation when Depreciation Value, Straight Line is higher than Depreciation Value, DDB. In period 8, Depreciation Value, DDB = 419.43. We still have 2097.15 - 1000 (see first picture, bottom half) to depreciate. If we use the Straight Line method this results in 3 remaining depreciation values of 1097.15 / 3 = 365.72. Depreciation Value, Straight Line is not higher so we do not switch. In period 9, Depreciation Value, DDB = 335.54. We still have 1677.72 - 1000 (see first picture, bottom half) to depreciate. If we use Straight line method this results in 2 remaining depreciation values of 677.72 / 2 = 338.86. Depreciation Value, Straight Line is higher so we switch to Straight Line calculation.

Note: the VDB function is much more versatile than the DDB function. It can calculate the depreciation value of multiple periods. In this example, =VDB(Cost,Salvage,Life,0,3) reduces to 2000 + 1600 + 1280 = 4880. It contains a 6th and 7th optional argument. You can use the 6th argument to use a different factor. If you set the 7th argument to TRUE it does not switch to Straight Line calculation (the same as DDB).

 

IRR function in Excel

 

Use the IRR function in Excel to calculate a project's internal rate of return. The internal rate of return is the discount rate that makes the net present value equal to zero.

Simple IRR example

For example, project A requires an initial investment of $100 (cell B5).

1. We expect a profit of $0 at the end of the first period, a profit of $0 at the end of the second period and a profit of $152.09 at the end of the third period.

Note: the discount rate equals 10%. This is the rate of return of the best alternative investment. For example, you could also put your money in a savings account at an interest rate of 10%.

2. The correct NPV formula in Excel uses the NPV function to calculate the present value of a series of future cash flows and subtracts the initial investment.

Explanation: a positive net present value indicates that the project’s rate of return exceeds the discount rate. In other words, it's better to invest your money in project A than to put your money in a savings account at an interest rate of 10%.

3. The IRR function below calculates the internal rate of return of project A.

4. The internal rate of return is the discount rate that makes the net present value equal to zero. To clearly see this, replace the discount rate of 10% in cell B2 with 15%.

Explanation: a net present value of 0 indicates that the project generates a rate of return equal to the discount rate. In other words, both options, investing your money in project A or putting your money in a high-yield savings account at an interest rate of 15%, yield an equal return.

5. We can check this. Assume you put $100 into a bank. How much will your investment be worth after 3 years at an annual interest rate of 15%? The answer is $152.09.

Conclusion: you can compare the performance of a project to a savings account with an interest rate equal to the IRR.

Present Values

For example, project B requires an initial investment of $100 (cell B5). We expect a profit of $25 at the end of the first period, a profit of $50 at the end of the second period and a profit of $152.09 at the end of the third period.

1. The IRR function below calculates the internal rate of return of project B.

2. Again, the internal rate of return is the discount rate that makes the net present value equal to zero. To clearly see this, replace the discount rate of 15% in cell B2 with 39%.

Explanation: a net present value of 0 indicates that the project generates a rate of return equal to the discount rate. In other words, both options, investing your money in project B or putting your money in a high-yield savings account at an interest rate of 39%, yield an equal return.

3. We can check this. First, we calculate the present value (pv) of each cash flow. Next, we sum these values.

Explanation: instead of investing $100 in project B, you could also put $17.95 in a savings account for 1 year, $25.77 in a savings account for 2 years and $56.28 in a savings account for three years, at an annual interest rate equal to the IRR (39%).

IRR rule

The IRR rule states that if the IRR is greater than the required rate of return, you should accept the project. IRR values are frequently used to compare investments.

1. The IRR function below calculates the internal rate of return of project X.

Conclusion: if the required rate of return equals 15%, you should accept this project because the IRR of this project equals 29%.

2. The IRR function below calculates the internal rate of return of project Y.

Conclusion: in general, a higher IRR indicates a better investment. Therefore, project Y is a better investment than project X.

3. The IRR function below calculates the internal rate of return of project Z.

Conclusion: a higher IRR isn't always better. Project Z has a higher IRR than project Y but the cash flows are much lower.

 

NPV formula in Excel

 

The correct NPV formula in Excel uses the NPV function to calculate the present value of a series of future cash flows and subtracts the initial investment.

Net Present Value

For example, project X requires an initial investment of $100 (cell B5).

1. We expect a profit of $0 at the end of the first period, a profit of $50 at the end of the second period and a profit of $150 at the end of the third period.

2. The discount rate equals 15%.

Explanation: this is the rate of return of the best alternative investment. For example, you could also put your money in a high-yield savings account at an interest rate of 15%.

3. The NPV formula below calculates the net present value of project X.

Explanation: a positive net present value indicates that the project’s rate of return exceeds the discount rate. In other words, it's better to invest your money in project X than to put your money in a high-yield savings account at an interest rate of 15%.

4. The NPV formula below calculates the net present value of project Y.

Explanation: the net present value of project Y is higher than the net present value of project X. Therefore, project Y is a better investment.

Understanding the NPV function

The NPV function simply calculates the present value of a series of future cash flows. This is not rocket science.

1. For example, project A requires an initial investment of $100 (cell B5). We expect a profit of $0 at the end of the first period, a profit of $0 at the end of the second period and a profit of $152.09 at the end of the third period.

Explanation: a net present value of 0 indicates that the project generates a rate of return equal to the discount rate. In other words, both options, investing your money in project A or putting your money in a high-yield savings account at an interest rate of 15%, yield an equal return.

2. We can check this. Assume you put $100 into a bank. How much will your investment be worth after 3 years at an annual interest rate of 15%? The answer is $152.09.

Note: the internal rate of return of project A equals 15%. The internal rate of return is the discount rate that makes the net present value equal to zero. Visit our page about the IRR function to learn more about this topic.

3. The NPV function simply calculates the present value of a series of future cash flows.

4. We can check this. First, we calculate the present value (pv) of each cash flow. Next, we sum these values.

Explanation: $152.09 in 3 years is worth $100 right now. $50 in 2 years is worth 37.81 right now. $25 in 1 year is worth $21.74 right now. Would you trade $159.55 for $100 right now? Of course, so project B is a good investment.

5. The NPV formula below calculates the net present value of project B.

Explanation: project B is a good investment because the net present value ($159.55 - $100) is greater than 0.

 

Loan Amortization Schedule in Excel

 

This example teaches you how to create a loan amortization schedule in Excel.

1. We use the PMT function to calculate the monthly payment on a loan with an annual interest rate of 5%, a 2-year duration and a present value (amount borrowed) of $20,000. We use named ranges for the input cells.

2. Use the PPMT function to calculate the principal part of the payment. The second argument specifies the payment number.

3. Use the IPMT function to calculate the interest part of the payment. The second argument specifies the payment number.

4. Update the balance.

5. Select the range A7:E7 (first payment) and drag it down one row. Change the balance formula.

6. Select the range A8:E8 (second payment) and drag it down to row 30.

It takes 24 months to pay off this loan. See how the principal part increases and the interest part decreases with each payment.